Congenital disorders
Graph theory applications in congenital heart disease
Abstract
Graph theory can be used to address problems with complex network structures. Congenital heart diseases (CHDs) involve complex abnormal connections between chambers, vessels, and organs. We proposed a new method to represent CHDs based on graph theory, wherein vertices were defined as the spaces through which blood flows and edges were defined by the blood flow between the spaces and direction of the blood flow. The CHDs of tetralogy of Fallot (TOF) and transposition of the great arteries (TGA) were selected as examples for constructing directed graphs and binary adjacency matrices. Patients with totally repaired TOF, surgically corrected d-TGA, and Fontan circulation undergoing four-dimensional (4D) flow magnetic resonance imaging (MRI) were included as examples for constructing the weighted adjacency matrices. The directed graphs and binary adjacency matrices of the normal heart, extreme TOF undergoing a right modified Blalock–Taussig shunt, and d-TGA with a ventricular septal defect were constructed. The weighted adjacency matrix of totally repaired TOF was constructed using the peak velocities obtained from 4D flow MRI. The developed method is promising for representing CHDs and may be helpful in developing artificial intelligence and conducting future research on CHD.
Introduction
Congenital heart diseases (CHDs) often involve abnormal connections between chambers, vessels, and organs, such as atrioventricular discordance, ventriculoarterial discordance, and cardiovascular shunts1. Management of CHDs may be related to the creation or elimination of the connections2,3. Graph theory is a branch of mathematics that can be applied to map complex networks between objects, and it is widely used in biomedical sciences4. Some studies have applied graph theory for the analysis of the human heart networks and have proposed its medical applications5,6,7,8,9,10. However, these studies have mainly focused on mathematical theories rather than on the pathophysiology of the heart. Moreover, the specific diseases and structural anomalies of the heart have not been considered. Therefore, this study developed a new method to represent CHDs based on graph theory.
Methods
Due to the retrospective nature of this study, the need of informed consent was waived by the National Taiwan University Hospital Research Ethics Committee. The study protocol strictly adheres to the ethical guidelines of the 1975 Declaration of Helsinki and was conducted in at a single tertiary referral hospital.
The definitions and terminologies used in graph theory are based on those in previous studies4,6. We denote the directed graph of the heart by G(V, E), where V is a set of vertices, and E is a set of edges between the vertices. Vertices are defined as the spaces through which blood flows and are numbered in order. Let V = {v1, v2,…, vi,…}; the vertices of the directed graph of the normal heart are assigned as follows: v1 = superior vena cava (SVC), v2 = inferior vena cava (IVC), v3 = right atrium (RA), v4 = right ventricle (RV), v5 = pulmonary trunk (PT), v6 = right pulmonary artery (RPA), v7 = left pulmonary artery (LPA), v8 = right lung (RL), v9 = left lung (LL), v10 = right upper pulmonary vein (RUPV), v11 = right lower pulmonary vein (RLPV), v12 = left upper pulmonary vein (LUPV), v13 = left lower pulmonary vein (LLPV), v14 = left atrium (LA), v15 = left ventricle (LV), v16 = ascending aorta (AAo), v17 = aortic arch (AoA), v18 = descending aorta (DAo), v19 = innominate artery (IA), v20 = left common carotid artery (LCCA), v21 = left subclavian artery (LSCA), v22 = right common carotid artery (RCCA), v23 = right subclavian artery (RSCA), and v24 = systemic circulation target organs (SCTO). We use vertex v24 to represent all organs involved in the systemic circulation, such as the brain, visceral organs, and soft tissues. Edges are defined as the blood flow between the spaces. If blood flows between two spaces, then an edge is formed between the two vertices. The direction of the edge is the direction of the blood flow. For example, if the blood flows from RA to RV, an edge is formed between v3 and v4 in the direction from v3 to v4.
Tetralogy of Fallot (TOF) is the most common cyanotic CHD, and patients with TOF sometimes require shunt creation, especially in the case of extreme TOF, which is characterized by pulmonary atresia2,11,12. Transposition of the great arteries (TGA) is a typical example of CHD with abnormal connections caused by ventriculoarterial discordance13. The most common form of TGA is d-TGA. Isolated d-TGA is incompatible with life without the presence of a shunt for blood mixing, and the most common shunt in d-TGA is a ventricular septal defect (VSD)14. Hence, we selected cases of extreme TOF managed using a right modified Blalock–Taussig (mBT) shunt and of d-TGA with a VSD as examples for constructing directed graphs.
We constructed adjacency matrices of the directed graph of the heart, including binary (unweighted) and weighted adjacency matrices. Let A = [aij] be a binary adjacency matrix of a graph G(V, E); aij equals “1” if there is an edge from vi to vj and “0” otherwise. For the heart, the connectivity weights can denote hemodynamic parameters such as flow, peak velocity, and pressure gradient. Echocardiography and cardiac magnetic resonance imaging (MRI) are common imaging modalities used to measure the aforementioned parameters15,16. In this study, we used four-dimensional (4D) flow MRI to construct the weighted adjacency matrices because the technique enables retrospective measurements of blood flows at arbitrary cross-sectional planes of a given vessel17. Patients with totally repaired TOF, surgically corrected d-TGA, and Fontan circulation undergoing 4D flow MRI were included as examples. Peak velocities of blood flows, which can be used to detect valvular, vascular, and anastomotic stenosis, were measured as weights in the weighted adjacency matrices by using 4D flow MRI18. Pulmonary stenosis is common in cases of totally repaired TOF and surgically corrected d-TGA. Hence, the peak velocities were measured between the RV, PT, RPA, and LPA. For the Fontan circulation, the peak velocities were measured between the SVC, RPA, IVC, and LPA to detect the potential anastomotic stenosis and increased pulmonary pressure.
Results
Directed graphs of the heart
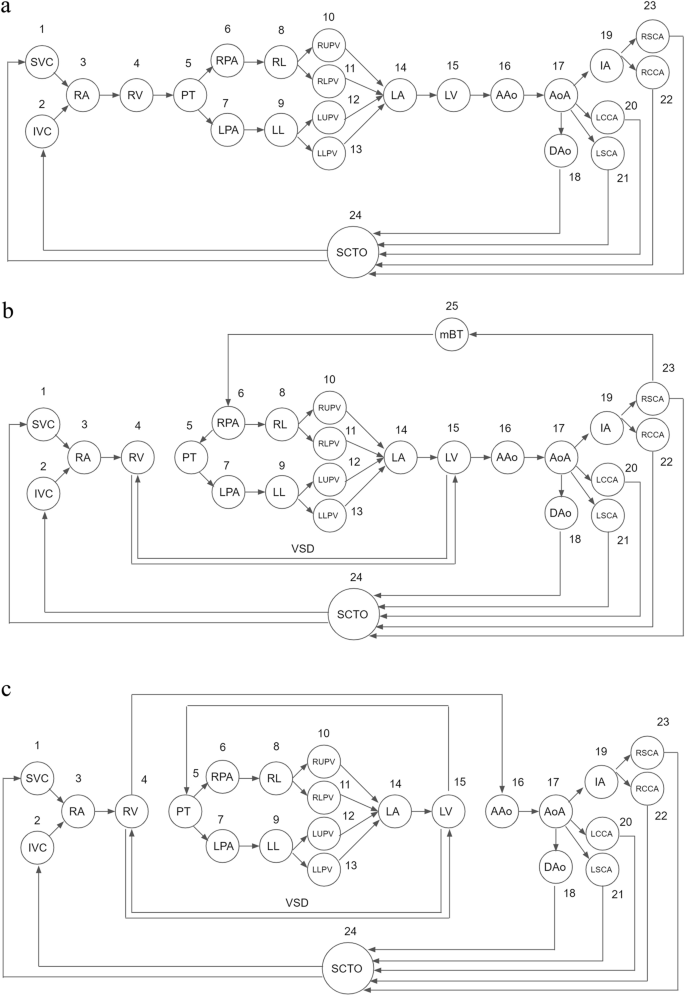
The directed graphs of the normal heart, extreme TOF undergoing a right mBT shunt, and d-TGA with a VSD are shown in Fig. 1. First, we drew the directed graph of the normal heart. Second, in the case of extreme TOF undergoing a right mBT shunt, the connection between the RV and PT was removed because of pulmonary atresia. An edge from the RV to LV and an edge from the LV to RV were added to the graph of the normal heart to represent VSD. Furthermore, the right mBT shunt was added to the graph as an additional vertex v25 = mBT shunt, which allowed blood flow from the RSCA to RPA first, and then to supply the bilateral lungs. The direction of the edge between PT and RPA was reversed due to the presence of pulmonary atresia and the blood flow supplied by the right mBT shunt. Finally, we drew the graph of d-TGA by eliminating the normal connections between the ventricles and great arteries (RV to PT, LV to AAo) and adding discordant connections (RV to AAo, LV to PT) to the graph of the normal heart. A VSD is mandatory to form the paths from systemic venous return (SVC, IVC) to the lungs (RL, LL) and the paths from the lungs to the arterial supply (AAo). This allows patients with d-TGA to return deoxygenated blood from the body, exchange gases in the lungs, and pump oxygenated blood to the systemic circulation that keeps survival.
Directed graphs of (a) the normal heart, (b) extreme TOF undergoing a right mBT shunt, and (c) d-TGA with a VSD. In the case of extreme TOF undergoing a right mBT shunt, the edge from the RV to PT is absent due to pulmonary atresia. The bidirectional edges between the RV and LV represent the VSD. An additional vertex, v25, represents the mBT shunt, which allows blood flow from the RSCA to the RPA to supply the lungs. The direction of the edge between PT and RPA was reversed due to the presence of pulmonary atresia and the blood flow supplied by the right mBT shunt. In the graph of d-TGA, the connections between the ventricles and great arteries are discordant (RV to AAo, LV to PT). A VSD forms the paths from systemic venous return (SVC, IVC) to the lungs (RL, LL) and the paths from the lungs to the arterial supply (AAo). This allows patients with d-TGA to return deoxygenated blood from the body, exchange gases in the lungs, and pump oxygenated blood to the systemic circulation. AAo ascending aorta, IVC inferior vena cava, LL left lung, LPA left pulmonary artery, LV left ventricle, mBT shunt modified Blalock-Taussig shunt, PT pulmonary trunk, RL right lung, RPA right pulmonary artery, RSCA right subclavian artery, RV right ventricle, SVC superior vena cava, TGA transposition of the great arteries, TOF tetralogy of Fallot, VSD ventricular septal defect.
Binary adjacency matrices of the hearts
The binary adjacency matrices of the normal heart, extreme TOF undergoing a right mBT shunt, and d-TGA with a VSD are shown in Fig. 2. Let B = [bij] and C = [cij] be the binary adjacency matrices of extreme TOF undergoing a right mBT shunt and d-TGA with a VSD, respectively. For the matrix of extreme TOF undergoing a right mBT shunt, an additional vertex caused the dimension of the matrix to increase from 24 × 24 to 25 × 25. The elements b23,25 = 1 and b25,6 = 1 represent the blood flow from RSCA to RPA via the right mBT shunt. The elements b4,15 = 1 and b15,4 = 1 represent the bidirectional VSD. The element b4,5 = 0 indicates pulmonary atresia. The elements b5,6 = 0 and b6,5 = 1 indicate the reversed blood flow from the RPA to the PT. For the matrix of d-TGA with a VSD, the elements c4,5 = 0 and c15,16 = 0 represent disconnection between the RV and PT, as well as between the LV and AAo, respectively. The elements c4,16 = 1 and c15,5 = 1 represent abnormal connections between the RV and AAo, as well as the LV and PT. In summary, these elements indicate ventriculoarterial discordance. The matrix of d-TGA can also be considered as the result of interchanging the 5th column (PT) and the 16th column (AAo) of the matrix of the normal heart.

Binary adjacency matrices of (a) the normal heart, (b) extreme TOF undergoing a right mBT shunt, and (c) d-TGA with a VSD. The values in the red boxes denote the differences between the binary adjacency matrices of the normal heart and CHDs. Let B = [bij] and C = [cij] be the binary adjacency matrices of extreme TOF undergoing a right mBT shunt and d-TGA with a VSD, respectively. For the matrix of extreme TOF undergoing a right mBT shunt, an additional vertex caused the dimension of the matrix to increase from 24 × 24 to 25 × 25. The elements b23,25 = 1 and b25,6 = 1 represent the blood flow from RSCA to RPA via the right mBT shunt. The elements b4,15 = 1 and b15,4 = 1 represent the bidirectional VSD. The element b4,5 = 0 indicates pulmonary atresia. The elements b5,6 = 0 and b6,5 = 1 indicate the reversed blood flow from the RPA to the PT. For the matrix of d-TGA with a VSD, the elements c4,5 = 0 and c15,16 = 0 represent disconnection between the RV and PT, as well as between the LV and AAo. The elements c4,16 = 1 and c15,5 = 1 represent abnormal connections between the RV and AAo, as well as the LV and PT. The matrix of d-TGA can also be considered as the result of interchanging the 5th column (PT) and the 16th column (AAo) of the matrix of the normal heart. AAo ascending aorta, CHD congenital heart disease, LV left ventricle, mBT shunt modified Blalock-Taussig shunt, PT pulmonary trunk, RPA right pulmonary artery, RSCA right subclavian artery, RV right ventricle, TGA transposition of the great arteries, TOF tetralogy of Fallot, VSD ventricular septal defect.
Weighted adjacency matrices of the hearts
The data of three patients who underwent 4D flow MRI and had three different conditions—totally repaired TOF, surgically corrected d-TGA, and Fontan circulation—were included. The process of constructing the weighted adjacency matrix for totally repaired TOF based on the results of 4D flow MRI is shown in Fig. 3. Regarding flow measurements, we usually only focus on a specific portion of the heart in clinical practice. Therefore, a submatrix of the binary adjacency matrix of the whole heart was selected to create the weighted adjacency matrix. In this case, we were interested in the peak velocities of blood flows between the RV, PT, RPA, and LPA. Initially, the peak velocities were measured at the boundaries of the spaces on 4D flow MRI (pulmonary valve and the origins of the RPA and LPA, the short white lines in Fig. 3) and were used as weights in the weighted adjacency matrix. Then, the submatrix including the vertices of interest was derived from the binary adjacency matrix of totally repaired TOF. After the weights and corresponding elements of the submatrix were combined, the weighted adjacency matrix of peak velocity was obtained. In the same way, the weighted adjacency matrices of surgically corrected d-TGA and Fontan circulation were constructed (Fig. 4).

Construction of the weighted adjacency matrix based on the results of 4D flow MRI. Blood flow visualization with velocity color-coded streamlines on 4D flow MRI. In the case of totally repaired TOF, we were interested in the peak velocities of blood flows between RV, PT, RPA, and LPA. The peak velocities (in cm/s) were measured at the boundaries of the spaces on 4D flow MRI (pulmonary valve and the origins of the RPA and LPA, the short white lines). The submatrix including the vertices of interest was derived from the binary adjacency matrix of totally repaired TOF (red box). After the weights and corresponding elements of the submatrix were combined, the weighted adjacency matrix of peak velocity was obtained. 4D flow MRI four-dimensional flow magnetic resonance imaging, LPA left pulmonary artery, PT pulmonary trunk, RPA right pulmonary artery, RV right ventricle, TOF tetralogy of Fallot.

Construction of the weighted adjacency matrices of (a) surgically corrected d-TGA and (b) Fontan circulation. Blood flow visualization with velocity color-coded streamlines on 4D flow MRI. The short white lines are the boundaries between adjacent structures where the peak velocities (in cm/s) are measured. Similar to totally repaired TOF, the peak velocities were measured between the RV, PT, RPA, and LPA in the case of surgically corrected d-TGA. For the Fontan circulation, the PT was separated from the RPA and LPA; the SVC and IVC were connected to RPA. The peak velocities were measured between the SVC, RPA, IVC, and LPA. The white arrow indicates the boundary between RPA and LPA, as well as the location of native pulmonary bifurcation. 4D flow MRI four-dimensional flow magnetic resonance imaging, IVC inferior vena cava, LPA left pulmonary artery, PT pulmonary trunk, RPA right pulmonary artery, RV right ventricle, SVC superior vena cava, TGA transposition of the great arteries, TOF tetralogy of Fallot.
Discussion
This study provided a representation of CHDs through graphs, binary and weighted adjacency matrices by using graph theory. We generated graph representations of the normal heart, TOF, and TGA. Based on the differences between the graph of the normal heart and that of CHDs, CHDs can be classified into five categories: (1) increased vertices; (2) decreased vertices; (3) increased edges; (4) decreased edges; and (5) abnormal connections. Examples for the five categories of binary adjacency matrices are shown in Table 1. The procedures to treat CHDs is also related to the addition and subtraction of these vertices and edges, as well as the correction of abnormal connections. Manifestations of the common surgical procedures in the binary adjacency matrices are shown in Table 2. For the CHDs and procedures associated with changes in vertices, we increased the dimensions of the adjacency matrices for the category of increased vertices while keeping the dimension unchanged for the category of decreased vertices. The reason for this is that a vertex is a chamber or a vascular structure with a real space and can connect to other vertices. Therefore, an additional vertex requires more dimension in the adjacency matrix to express the possible connections with all the other vertices. By contrast, the absence of a vertex can be expressed by eliminating all the edges connected to the vertex. Thus, isolating the vertex from the other vertices is equivalent to removal of the vertex from the graph in our cases.
Our methods for defining the vertices and edges of the graph are similar to those used in studies on graph theory applications in the human heart5,6,7,8. However, our models are more detailed and practical than those used in previous studies. For example, our model comprised four vertices to represent four pulmonary veins. This design is crucial for describing anomalous pulmonary venous return but has been rarely used in other studies. In addition, most previous models have only included the cardiovascular structures from the vena cavae to the aorta. By contrast, we included the structures from the vena cavae to the branches of the aorta because the branches include the innominate artery, carotid arteries, and subclavian arteries, which also play a role in CHDs and are often associated with additional blood supply to the lungs, such as mBT shunt and systemic-to-pulmonary collateral arteries. Moreover, we added the vertex of SCTO to complete the circuit of the entire circulatory system. Abnormalities in the connections between systemic arterial supply, SCTO, and systemic venous return are usually associated with cardiovascular diseases in adults such as atherosclerotic occlusive diseases, arterial dissections, deep vein thrombosis, and SVC syndrome. The aim of this study was not to establish the standard graph representation of the human heart but to propose a feasible model. Various graph representations can be adopted depending on the purpose. For instance, if information on more detailed structures, such as coronary arteries, segments of the aorta, and pulmonary arteries, is required, more vertices can be added into the graph. Moreover, the graph representations can include dynamic changes obtained from imaging modalities such echocardiography and cardiac MRI. Finite-state machine may be used to describe the dynamic changes of blood flow, chamber and vessels in the cardiac cycle19,20.
In addition to the human heart, graph theory has been applied to other systems and organs in the human body. One of the most important applications of graph theory is the connectome in neuroscience. Since the coining of the term connectome in 2005, the number of related studies has markedly increased, with more than 1000 publications per year over the past few years21. Graph theoretical analysis of complex brain networks reveals that the human connectome can be a diagnostic marker of several neurodegenerative and psychiatric diseases22. Graph theory is also used to build models of brain vessels, the hepatic portal system, the glomerular capillary network, and the lymphatic system23,24,25,26,27,28,29.
The increasing survivorship of patients with CHD increases the prevalence of CHD, and as a result, physicians without having training in CHD may need to manage these patients30. Graph representation simplifies the complex cardiovascular structures and makes them easier to understand for the physicians and patients. Furthermore, according to previous graph theory-based studies, we propose some applications of our CHD model.
Artificial intelligence in CHD
If there is an artificial intelligence model capable of segmenting the cardiovascular structures in CHDs on the imaging, we can obtain the boundaries of these structures and detect the blood flow between them. By doing so, we can establish the connections between these structures and construct the graphs of the hearts. By comparing these graphs with the established graphs of CHDs in this study, we can obtain the diagnoses for the congenital heart diseases of the hearts. For example, if the morphologic RA, RV, LA, LV, AAo and PT can be automatically identified and segmented on MRI, atrioventricular and ventriculoarterial connections can be established using 4D flow MRI. If blood flow is detected from the RV to the AAo and from the LV to the PT, the diagnosis of TGA can be made (Fig. 1c). Furthermore, through 4D flow MRI and appropriate segmentation of cardiovascular structures, hemodynamic abnormalities such as regurgitation and increased velocity due to vascular stenosis can be automatically detected. Although the automatic segmentation and classification of CHD in medical imaging are challenging due to the complex cardiovascular structures involved, with advances in machine learning techniques, many feasible models have been proposed31,32,33.
For automatic segmentation, graph matching, which is a graph theory-based technique, has been adopted to improve the performance of deep learning models. Graph matching in a previous study involved the construction of a graph library to describe all possible connections between great vessels32. Various graph representations and categories of CHDs demonstrated in the present study can be used to establish a comprehensive graph library and can facilitate the development of deep learning in CHD.
Connectome of the heart
Similar to the application of the connectome in the neurological disorders, graph representations of the heart can be applied to heart diseases34. In this study, we demonstrated that the changes in the numbers of vertices, edges, and connections were associated with the structural or hemodynamic abnormalities of the heart. In addition, imaging modalities such as echocardiography and cardiac MRI, similar to electroencephalography, diffusion tensor imaging, and functional MRI in neuroscience, can be used to construct weighted adjacency matrices, which can store the hemodynamic parameters of the heart in the matrices and enable further analysis to find unknown relationships between the matrices and heart diseases35,36,37.
Finding unknown types, pathophysiology, and treatments of CHDs
The number of all possible directed graphs with 24 vertices is 2(24×23)–1.47 × 10166, which is considerably more than the types of CHDs currently known. This observation implies that some cardiovascular structures of the possible directed graphs have not yet been discovered or reported, while some cardiovascular structures cannot exist due to certain reasons. We can find unknown types of CHDs through the following steps: (1) given 24 vertices, as defined above, generate all possible directed graphs; (2) exclude the known CHDs based on our knowledge and literal searches on databases such as PubMed and Google Scholar; (3) the remaining non-excluded directed graphs are the possible unknown cardiovascular structures of CHDs. For each possible unknown cardiovascular structure, we can use our knowledge of physiology and embryology to determine the existence of this cardiac structure. A well-known rule for patients with CHDs to survive is “there exists a lung such that a path from the systemic venous return to the lung and a path from the lung to the systemic arterial supply”, which we can see in the patients with extreme TOF and d-TGA14. For instance, if a patient has d-TGA without a VSD, there is no blood flow between the RV and the PT. The deoxygenated blood from the systemic venous return (SVC, IVC) flows into the RV and is then pumped directly into the systemic arterial supply (AAo) without undergoing gas exchange in the lungs (Fig. 1c). The patient cannot survive due to a lack of oxygenated blood in the systemic circulation. In addition, other unknown factors may also affect survival of CHD. Therefore, scrutinizing all possible cardiovascular structures by using our model, we may find unknown CHDs and unknown rules associated with the existence of CHDs, that is, (cardiovascular structures of all possible directed graphs with the given vertices) − (known cardiovascular structures) − (abnormal cardiovascular structures incompatible with life because of the known rules) = (abnormal cardiovascular structures compatible with life but not reported yet) + (abnormal cardiovascular structures incompatible with life because of unknown rules). For example, congenital anomalies such as congenital total absence of SVC and congenital aortocaval fistula to the SVC are extremely rare anomalies and have never been recorded in some institutes38,39. However, the existence of the anomalies can be predicted using our model. Furthermore, the procedures for treatment of CHDs such as mBT shunt, Norwood procedure, bidirectional Glenn shunt and Fontan procedure can also be derived from our model. The unknown treatments of CHDs may be discovered in all possible directed graphs with the given vertices.
The proposed graph representations of CHDs have some limitations. They cannot describe abnormal spatial relationships between cardiovascular structures such as the situs inversus, L-loop, overriding aorta, right aortic arch, aberrant subclavian artery, retroaortic left innominate vein, and anomalous course of coronary arteries. Some spatial relationships may be represented by adding new vertices based on embryology40,41. Moreover, a binary adjacency matrix cannot describe two edges with the same origin vertex, destination vertex and direction. Further research is needed to find the more general graph models to describe CHDs.
In conclusion, graph theory can be used to represent CHDs, which may be helpful for developing artificial intelligence and conducting future research on CHD.
Data availability
The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.
References
-
Lapierre, C. et al. Segmental approach to imaging of congenital heart disease. Radiographics 30, 397–411 (2010).
Google Scholar
-
Gladman, G., McCrindle, B. W., Williams, W. G., Freedom, R. M. & Benson, L. N. The modified Blalock-Taussig shunt: Clinical impact and morbidity in Fallot’s tetralogy in the current era. J. Thorac. Cardiovasc. Surg. 114, 25–30 (1997).
Google Scholar
-
Norwood, W. I. Jr., Jacobs, M. L. & Murphy, J. D. Fontan procedure for hypoplastic left heart syndrome. Ann. Thorac. Surg. 54, 1025–1030 (1992).
Google Scholar
-
Pavlopoulos, G. A. et al. Using graph theory to analyze biological networks. BioData Mining 4, 1–27 (2011).
Google Scholar
-
Shokry, M. & Aly, R. E. Topological properties on graph vs medical application in human heart. Int. J. Appl. Math. 15, 1103–1108 (2013).
-
Basavaprasad, B. & Ravindra, S. H. A graph theoretical network model on human heart. Int. J. Appl. Eng. Res. 9, 4549–4553 (2014).
-
Nawar, A. S. & El Atik, A. E. F. A. A model of a human heart via graph nano topological spaces. Int. J. Biomath. 12, 1950006 (2019).
Google Scholar
-
Abeyrathne, R. & Lanel, G. A study on graph theory properties in human blood circulatory system. Int. J. Sci. Res. Publ. 11, 444. https://doi.org/10.29322/IJSRP.11.10.2021.p11851 (2021).
Google Scholar
-
Othman, H. A. et al. Pathless directed topology in connection to the circulation of blood in the heart of human body. AIMS Math. 7, 18158–18172 (2022).
Google Scholar
-
El Atik, A. E. F. A. A topological approach of a human heart via nano pre-ideality. Thai J. Math. 20, 1273–1285 (2022).
Google Scholar
-
Apitz, C., Webb, G. D. & Redington, A. N. Tetralogy of fallot. The Lancet 374, 1462–1471 (2009).
Google Scholar
-
Coelho, E. et al. Tetralogy of Fallot: Angiocardiographic, electrocardiographic, vectorcardiographic and hemodynamic studies of the Fallot-type complex. Am. J. Cardiol. 7, 538–564 (1961).
Google Scholar
-
Van Praagh, R. Terminology of congenital heart disease. Glossary and commentary. Circulation 56, 139–143 (1977).
Google Scholar
-
Warnes, C. A. Transposition of the great arteries. Circulation 114, 2699–2709. https://doi.org/10.1161/circulationaha.105.592352 (2006).
Google Scholar
-
Di Salvo, G. et al. Imaging the adult with congenital heart disease: A multimodality imaging approach—Position paper from the EACVI. Eur. Heart J.-Cardiovasc. Imaging 19, 1077–1098 (2018).
Google Scholar
-
Sachdeva, S. & Gupta, S. K. Imaging modalities in congenital heart disease. Indian J. Pediatr. 87, 385–397 (2020).
Google Scholar
-
Azarine, A. et al. Four-dimensional flow MRI: Principles and cardiovascular applications. Radiographics 39, 632–648 (2019).
Google Scholar
-
Jacobs, K. et al. Hemodynamic assessment of structural heart disease using 4D flow MRI: How we do it. Am. J. Roentgenol. 217, 1322–1332 (2021).
Google Scholar
-
Zhang, Z., Xia, C., Fu, J. & Chen, Z. Initial-state observability of mealy-based finite-state machine with nondeterministic output functions. IEEE Trans. Syst. Man Cybern. Syst. 52, 6396–6405 (2022).
Google Scholar
-
Zhang, Z., Shu, S. & Xia, C. Networked opacity for finite state machine with bounded communication delays. Inf. Sci. 572, 57–66 (2021).
Google Scholar
-
Veldhuizen, M. G. et al. Future directions for chemosensory connectomes: Best practices and specific challenges. Front. Syst. Neurosci. 54, 5304 (2022).
-
Bullmore, E. & Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).
Google Scholar
-
Paetzold, J. C. et al. Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2).
-
Reichold, J. et al. Vascular graph model to simulate the cerebral blood flow in realistic vascular networks. J. Cereb. Blood Flow Metab. 29, 1429–1443 (2009).
Google Scholar
-
El Azab, M. S., Shokry, M. & Emad Aly, R. A new view of special types of subgraphs with applications on circulation of hepatic portal system. Inf. Sci. Lett. 11, 215 (2022).
Google Scholar
-
Wahl, E. M., Daniels, F. H., Leonard, E., Levinthal, C. & Cortell, S. A graph theory model of the glomerular capillary network and its development. Microvasc. Res. 27, 96–109 (1984).
Google Scholar
-
Savinkov, R. et al. Graph theory for modeling and analysis of the human lymphatic system. Mathematics 8, 2236 (2020).
Google Scholar
-
Tretyakova, R., Savinkov, R., Lobov, G. & Bocharov, G. Developing computational geometry and network graph models of human lymphatic system. Computation 6, 1 (2017).
Google Scholar
-
Mozokhina, A. & Savinkov, R. Mathematical modelling of the structure and function of the lymphatic system. Mathematics 8, 1467 (2020).
Google Scholar
-
Hoffman, J. I. E., Kaplan, S. & Liberthson, R. R. Prevalence of congenital heart disease. Am. Heart J. 147, 425–439. https://doi.org/10.1016/j.ahj.2003.05.003 (2004).
Google Scholar
-
Pace, D. F. et al. International Conference on Medical Image Computing and Computer-Assisted Intervention 80–88 (Springer).
-
Xu, X. et al. International Conference on Medical Image Computing and Computer-Assisted Intervention 477–485 (Springer).
-
Xu, X. et al. International Conference on Medical Image Computing and Computer-Assisted Intervention 77–87 (Springer).
-
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M. & Scheltens, P. Small-world networks and functional connectivity in Alzheimer’s disease. Cereb. Cortex 17, 92–99. https://doi.org/10.1093/cercor/bhj127 (2007).
Google Scholar
-
Vecchio, F., Miraglia, F. & MariaRossini, P. Connectome: Graph theory application in functional brain network architecture. Clin. Neurophysiol. Pract. 2, 206–213. https://doi.org/10.1016/j.cnp.2017.09.003 (2017).
Google Scholar
-
Iturria-Medina, Y. et al. Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. Neuroimage 36, 645–660. https://doi.org/10.1016/j.neuroimage.2007.02.012 (2007).
Google Scholar
-
Salvador, R. et al. Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex 15, 1332–1342. https://doi.org/10.1093/cercor/bhi016 (2005).
Google Scholar
-
Oliveira, J. D. & Martins, I. Congenital systemic venous return anomalies to the right atrium review. Insights Imaging 10, 115. https://doi.org/10.1186/s13244-019-0802-y (2019).
Google Scholar
-
Soler, P., Mehta, A. V., Garcia, O. L., Kaiser, G. & Tamer, D. Congenital systemic arteriovenous fistula between the descending aorta, azygos vein, and superior vena cava. Chest 80, 647–649. https://doi.org/10.1378/chest.80.5.647 (1981).
Google Scholar
-
Tong, E., Rizvi, T. & Hagspiel, K. D. Complex aortic arch anomaly: Right aortic arch with aberrant left subclavian artery, fenestrated proximal right and duplicated proximal left vertebral arteries-CT angiography findings and review of the literature. Neuroradiol. J. 28, 396–403. https://doi.org/10.1177/1971400915598075 (2015).
Google Scholar
-
Gerlis, L. M. & Ho, S. Anomalous subaortic position of the brachiocephalic (innominate) vein: A review of published reports and report of three new cases. Heart 61, 540–545 (1989).
Google Scholar
Acknowledgements
The authors would like to thank all colleagues who contributed to this study. The work was supported by the Good Liver Foundation.
Author information
Authors and Affiliations
Contributions
Y.-T.L. and S.-J.C. are responsible for the overall content, including planning of the work, data collecting and drafting the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Lee, YT., Chen, SJ. Graph theory applications in congenital heart disease.
Sci Rep 13, 11135 (2023). https://doi.org/10.1038/s41598-023-38233-3
-
Received: 21 April 2023
-
Accepted: 05 July 2023
-
Published: 10 July 2023
-
DOI: https://doi.org/10.1038/s41598-023-38233-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.