Blood
An analytical method informed by clinical imaging data for estimating outlet boundary conditions in computational fluid dynamics analysis of carotid artery blood flow
Abstract
Stroke occur mainly due to arterial thrombosis and rupture of cerebral blood vessels. Previous studies showed that blood flow-induced wall shear stress is an essential bio marker for estimating atherogenesis. It is a common practice to use computational fluid dynamics (CFD) simulations to calculate wall shear stress and to quantify blood flow. Reliability of predicted CFD results greatly depends on the accuracy of applied boundary conditions. Previously, the boundary conditions were estimated by varying values so that they matched the clinical data. It is applicable upon the availability of clinical data. Meanwhile, in most cases all that can be accessed are arterial geometry and inflow rate. Consequently, there is a need to devise a tool to estimate boundary values such as resistance and compliance of arteries. This study proposes an analytical framework to estimate the boundary conditions for a carotid artery based on the geometries of the downstream arteries available from clinical images.
Introduction
Atherosclerosis is one of the main reasons for suffering a stroke and it is the world’s major cerebrovascular disease1. Atherosclerosis is defined as the build-up of fatty materials on the inner wall lining of arteries which turns into atherosclerotic plaque and eventually results in the cross-sectional area of the arterial lumen diminishing2. The prime sites of atherosclerosis inside the arterial lumen are locations with high flow disturbances leading to either low wall shear stress (WSS) regions or unstable oscillatory shear stress regions3. The likelihood of plaque formation and atherosclerosis initiation is high for a region with WSS less than 0.4 Pa in the carotid arteries4,5,6. Thus WSS is an important bio marker for determining when atherosclerosis commences, and rupture of cerebral arteries. Arterial geometric factors and blood flow conditions greatly shape the hemodynamic characteristics of blood flow such as blood viscosity, cardiac output, and distal vascular resistance7. Complicated and disturbed blood flow is reported in the regions with complex geometry in the cardiovascular systems such as curvatures and bifurcations8. Thus the hemodynamics of blood vessels constitute an important aspect of biomedical and biomechanical engineering because the clinical consequences are substantial.
Computational fluid dynamics (CFD) is considered one of the most reliable, non-invasive, and inexpensive approaches in the current scientific environment for understanding the hemodynamics of complex arterial regions such as the carotid artery. It can provide an accurate approximation of velocity, pressure and wall shear stress distributions through a 3D visible representation which is otherwise difficult to obtain by non-invasive techniques9,10. CFD simulations can provide better insights into the hemodynamics of regions that are complex and not accessible to physical measurement. Since CFD results have shown good agreement with in vivo results, it is deemed to be the better alternative to physical experiments in studying hemodynamics because of the high cost and time involved in experiments11,12. Boundary conditions are very crucial in determining the accuracy of numerical simulations since the selection of boundary conditions wields a high influence on the flow field generated in CFD simulations13,14.
Realistic boundary conditions are also one of the prime important factors in the CFD set-up for calculating accurately the pressure, velocity fields and wall shear stress15,16. Outlet boundary conditions incorporate hemodynamic characteristics of downstream vascular elements such as capillaries, arterioles, arteries, veins, and venules15. Most previous studies give constant velocity, zero pressure, constant pressures, pressure gradient, and constant resistance to the outlet of carotid arteries for convenience. However, the results will not be realistic as they neglect the key distal vascular characteristics, i.e. resistance, impedance, and compliance. The more realistic boundary condition should encompass the natural wave reflections arising from branchings and other geometrical features which are capable of propagating upstream elements. It is also reported that the choice of outflow boundary conditions has important ramifications for the distribution of flow parameters such as pressure field and velocity field along with characteristics of pressure/flow wave propagation15,17. Thus, the incorporation of precise outlet boundary conditions plays a prominent role in CFD simulations in providing accurate physiology of blood flow at the carotid artery.
The Windkessel model is a prominent outflow boundary model employed in arterial blood flow simulation studies. It incorporates distal vascular characteristics as outlet boundary conditions into the CFD domain18,19,20,21,22,23,24,25,26. This model is a lumped parameter invention developed by Otto Frank in 1899 to represent the hemodynamics of the arterial network by reproducing physiological relationships between hemodynamic characteristics such as blood flow rate and pressure24,27. This lumped parameter model is analogous to an electrical circuit in which arterial blood pressure and flow are represented by electrical voltage and current, respectively23,28. The Windkessel model is either represented as 2, 3 or 4-element models in terms of resistance, compliance, impedance and inertance using various electrical circuit analogue elements, for instance resistor, capacitor, and inductor. The arrangement of these elements determines the excellence of the reproduced physiological relationship between blood pressure and flow features in the distal vascular elements of the arterial network, taking into account the vessel properties and flow features24,27,29. One of the main advantages of using the Windkessel model is its ability to estimate the reaction of distal vascular elements to potential changes in the blood flow by providing the hemodynamic relationship between pressure and flow waves. It is otherwise very difficult to obtain using invasive pressure measuring techniques in clinical practice29.
Pengcheng et al.9 conducted an assessment study on different outlet boundary conditions such as the Windkessel model, structured-tree model and fully developed flow model on the carotid artery. They concluded that the Windkessel model appears to be the more accurate and better-performing one, considering all statistical analyses and compared with invasive pressure measurements and Ultrasound Doppler Velocimeter velocity measurements. Olufsen et al. employed a simplified 3-element Windkessel model of blood flow in cerebral arteries to analyse changes in the peripheral and systemic resistance. They asserted that using a simplified lumped parameter model provides easy extraction of dynamic variations of required parameters compared to clinical data. In this way validation is an easier process. They also added that utilising basic models can lead to essential changes in the desired parameters which are otherwise very tedious when using complex lumped parameter models30. In a recent study, blood flow in the carotid artery was modelled using the 0D lumped parameter approach in a healthy and stenosed case that depicted a good match between blood flow simulation results and blood flow measurements. This study concluded that analysis of hemodynamics in the carotid artery using the 0D lumped parameter model is an acceptable approach31. Another study used a 4-element Windkessel model to assess the blood pressure waveform in the carotid artery for different blood pressure conditions such as normotensive, pre-normotensive and hypertensive. Obtained here were results that matched well with previous studies23.
The hemodynamic characteristics such as blood flow rate, blood viscosity and vascular compliance in a cerebrovascular system are also represented by distal vascular resistance. Increasing distal vascular resistance will reduce the blood flow rate in arteries which leads to an increase in the arterial diameter by arterial deformation. Lee et al.7 reported that during the systolic phase, the low wall shear stress area increased by 5% for a 20% increase in distal vascular resistance. Transient blood flow simulation conducted on carotid bifurcation reveals that high distal vascular resistance will result in low wall shear stress regions in the carotid artery leading to atherosclerosis progression37. Arterial compliance represents the vascular deformation of cerebral arteries in the form of arterial wall motion due to the pulsatile motion of blood flow inside arteries32,33,34. Onaizah et al. discovered that pressure waveforms at the inlet of common carotid artery (CCA) and mean blood flow rate and flow fraction via internal carotid artery (ICA) are impacted by local variations in the carotid artery compliance which in turn affects the supply of blood to the brain. They reported a higher mean blood flow rate at ICA when the compliance in the carotid artery rose when maintaining a fixed flow rate at CCA35.
Previous studies have used a tedious and time-consuming process to calculate Windkessel parameters by adjusting resistance and compliance values until they match clinical results. To overcome these challenges, researchers can estimate the Windkessel parameters by mapping the distal vascular elements of the carotid artery, which requires knowledge of the carotid artery’s geometrical and anatomical features. However, to date, no research has mapped these features for Windkessel parameter estimation using analytical methods.
This study aims to fill this gap by mapping the distal vascular elements of the internal carotid artery (ICA) and external carotid artery (ECA), calculating the resistance and compliance of each branch and sub-branch of the carotid artery analytically, and validating the results using clinical data through CFD simulations. The values of the Windkessel parameters can serve as initial values for iteration purposes to match hemodynamic parameters measured from CFD studies with clinical data, which can significantly reduce the time spent on iteration purposes.
The data provided in this study can be a great aid to researchers interested in exploring the hemodynamics of the distal cerebral vascular system, as it gives detailed step-by-step values of resistance and compliance at many intersections and divisions along the distal sections of the ACA and MCA. This level of detail is not currently available in the literature and can greatly benefit researchers in the field. The Windkessel parameters for the distal branches of the carotid artery calculated in this study through analytical methods are very relevant in obtaining more accurate CFD results compared to studies that use simplified outlet boundary conditions such as constant pressure, flow splits, and constant velocity. Additionally, this study provides an easier option to establish the resistance and compliance of the distal branches of the carotid artery, which is otherwise a tedious, time-consuming, and computationally costly operation that requires various iterations until matching with clinical results is achieved.
Methodology
Geometry and anatomy of different parts of the carotid artery
Carotid arteries are one of the most important parts of the cerebral vascular system since they carry oxygen-rich blood from the heart to the head and brain. The carotid artery originates from the aorta of the heart and is divided into three main regions: the Common Carotid Artery (CCA) which bifurcates into the Internal Carotid Artery (ICA) and the External Carotid Artery (ECA). The branching of the carotid artery takes place in the widening of the carotid artery called a carotid sinus or carotid bulb. ICA supplies blood to the brain whereas ECA supplies blood to the face. Two carotid arteries are located on the left- and right-hand sides of the human neck and are called the Left Carotid Artery and Right Carotid Artery, respectively36,37. In this study, We have used information about geometry of different parts of carotid artery and its distal branches from various previously published clinical images and data. No human is directly involved, and no private human data is used for this study.
ICA
There are many classifications of the segments of ICA and branches arising from these segments of ICA. According to the recent and most popular classification by Bouthillier et al., ICA is divided into 7 segments and 10 major branches. The segments of ICA are cervical, Petrous, Lacerum, Cavernous, Clinoid, Ophthalmic and Communicating segments, whereas major branches arising from these segments are Caritocotympanic Artery, Vidian Artery, Meningeal Artery, Inferior Hypophyseal Artery, Superior Hypophyseal artery, Ophthalmic Artery, Posterior Communicating Artery, Anterior Choroidal Artery, Anterior Cerebral Artery and Middle Cerebral Artery38. In this study, the main focus is on estimating the Windkessel parameters for Middle Cerebral Artery (MCA), Anterior Cerebral Artery (ACA) and the Ophthalmic Artery. The mean length of the ICA reported in one study considering the length from the proximal cavernous segment to the terminus of ICA was 33.1 ± 6.1 mm. The same study reported a mean diameter of 5 ± 0.60 mm and 3.6 ± 0.4 mm at the cavernous and the terminus segments, respectively39. MCA and ACA are the terminal branches of ICA.
MCA
MCA is the wider terminal branch of the ICA which extends from the base to the lateral surface of the brain through the lateral sulcus of Sylvius supplies blood to the lateral cerebral hemisphere, insula, temporal pole, lentiform nucleus, internal capsule and other deep structures of the brain40. Based on the anatomic structures and surgical classifications, MCA is divided into four segments which extend in a step-by-step angular manner: M1 (sphenoidal segment), M2 (insular segment), M3 (opercular segment), and M4 (cortical segment). There are 10 main branches arising out of these segments and they are as follows: lateral lenticulostriate arteries, anterior temporal arteries, orbitofrontal arteries, prefrontal arteries, precentral arteries, central arteries, postcentral arteries, parietal arteries, angular arteries and middle temporal arteries40,41.
The M1 segment originates in the Sylvian cistern at the terminal bifurcation of the ICA travelling parallel to the sphenoid ridge inside the proximal Sylvian fissure40,42. One research study reported the mean diameter of M1 as 3.49 mm43. Reci et al. reported variations in the length, shape and branching of M1 segment in 50 different specimens. As per this study, 64% of M1 segments are arch-shaped with an average length and diameter of 19.8 ± 4.41 mm and 2.6 ± 0.47 mm respectively. Conversely, 24% is S-shaped with proportions of 20.6 ± 3.31 mm (length), 2.7 ± 0.51 mm (diameter) and 12% is straight-shaped with a length of 16.9 ± 3.62 mm and diameter of 2.6 ± 0.36 mm44. Average length and diameter for the M1 segment were calculated based on information from the above article, i.e. 19.644 mm in length and 2.664 mm in diameter.
The major branches of the M1 segment are anterior temporal arteries (ATA) and lateral lenticulostriate arteries (LSA). Both arteries are located on opposite sides of the M1 segment with lenticulostriate arteries on the front side and ascend before M2s bifurcation whereas ATA is on the rear side40. The LSAs are generally 6–12 in number with each branch diameter ranging from 0.08 mm to 1.4 mm with a mean diameter of 0.47 mm. The average length of LSAs is 21.9 mm45. In this study, LSAs are assumed to be 9 in total considering the average number of branches. The diameter of ATAs ranges from 1.5 to 2 mm with an average value of 1.75 mm as applied in this study46.
Previous studies show that 78% of the M1 segment bifurcates into superior and inferior trunks of M2 segments, while 12% trifurcates into superior, inferior, and middle trunks of M2 segments. The remaining 10% divides into various smaller superior and inferior terminal branches. These bifurcations and trifurcations exist mainly at the insular cistern after M1 makes a sharp turn around the front end of the limen insula resulting in M2 branches located in the frontal end of the insula. Major superior terminal branches are the prefrontal sulcal artery, lateral frontonasal artery, Rolandic (central) sulcal and pre-Rolandic (precentral) artery. Major inferior terminal branches are the temporal artery, angular artery and parietal arteries40,42. In this study, M1 bifurcates into two trunks of M2 with ATA added along with the bifurcation since it is located towards the rear of the M1–M2 intersection. The M2 segments generally have 8–12 branches40, but in this study the majority of those branches are neglected as their size is very negligible. In addition, the lack of authentic geometric measurements of these branches also forced us to neglect these. One study reported M2 branches as having an average diameter of 2.4 ± 0.4 mm39 whereas another analysis documented mean diameter of M2 ranging from 1.4 to 2.3 mm, and the mean length varied from 12.1 to 14.9 mm47. In this study, M2 diameter and length are assumed to be 2.4 mm and 13.5 mm, respectively, taking in account popular opinion and average values noted in previous studies.
The M2 segments after taking an oblique turn through the opercular extension of the Sylvian fissure form the M3 segment of MCA. An accurate geometric estimation of the length and diameter of M3 has not yet been correctly reported. In that case, in this study, an average diameter of 1.7 mm and length of 13.3 mm is assumed for the M3 segment considering the mean diameter and length of adjacent segments M2 and M4. M3 segments after taking a right angle turn forms the M4 segments in the cortex region. One study reported the diameter of the cortical segment as 1 mm with segment length ranging from 0 to 40 mm with a mean length of 13.1 mm48. It is reported that 6 to 13 branches arise from the M4 cortical segment which includes orbitofrontal, prefrontal, precentral, central, temporopolar, anterior temporal, middle temporal, posterior temporal, and temporo-occipital, anterior parietal, angular and posterior parietal arteries49.
In this study, 3 main branches of the M4 segment are considered and they are the lateral orbitofrontal artery (LOFA), angular artery and temporopolar artery. These branches are considered major ones in cortical segments in many studies47,48. The angular artery is the largest vessel in the M4 segment on both sides of the brain with a mean diameter of 1.5 mm whereas the temporopolar artery is the smallest with a mean diameter of 0.8 mm and 0.9 mm on the right and left hemispheres, respectively47. In this study, an average value of 0.85 mm is assumed for the temporopolar artery. The lateral orbitofrontal artery is found to range from 2 to 40 numbers with an average number of 15.78 ± 10.44 for supply to the lateral orbitofrontal cortex48. In this paper, 16 branches of LOFA are considered. A previous study reported an average diameter of 0.8 mm for LOFA from a range of 0.4–1.5 mm and an average length of 13.1 mm from a range of 0–40 mm48,50. In this study, both angular artery and temporopolar artery are assumed to have the same segment length of LOFA due to the lack of credible medical data.
ACA
The anterior cerebral artery (ACA) is also a terminal branch of the ICA which supplies blood to the interhemispheric region. The ACA is mainly divided into two parts called proximal parts (A1) and distal parts (A2 to A5)51. ACA segment before and after the anterior communicating artery (AComA) is known as the proximal parts and distal parts, respectively. The distal section of ACA contains cortical and central branches and is also called the pericallosal artery51,52. The mean diameter of ACA at origin was reported as 2.61 ± 0.34 mm while its mean length from vessel origin to AComA is 7.68 ± 3.91 mm in the orbitofrontal region. Conversely, 112.6 ± 11.63 mm in the inferior internal parietal region was reported52. In this study, the mean length of ACA in the orbitofrontal region is noted. ACA is mainly divided into 5 segments, i.e. A1–A5. A1 segment is also called a pre-communicating or horizontal segment. It commences from the terminal bifurcation of ICA with a segment length of 14 mm and mean diameter of 2.6 mm51.
The main branches that arise from the A1 segment are AComA and medial lenticulostriate arteries53. Sousa et al.51 reported that the AComA arises from the terminals of the A1 segment with a mean diameter of 1.6 mm and a mean length of 2–3 mm; however, the length of AComA varies from 0.3 to 7 mm. In another study, the exposed length of ACA is determined as 3 ± 2 mm and 3.3 mm54,55. Considering the mean values in both studies, in this study the mean length of AComA is 3 mm. The AcomA contains perforating branches called Subcallosal-Hypothalamic Perforating Branches and their average number is 7.6 (range from 4 to 15) and a diameter of 0.4 ± 0.2 mm (0.1–1 mm range)56. The median callosal artery also originates from AComA with a mean diameter of 0.75 mm (range 0.5–1 mm)57. The length of these perforating branches and arteries in the AcomA is assumed to be 5 mm when the geometric features of nearby arteries are considered. The medial lenticulostriate arteries are 2 to 15 in number and are reported to be shorter in length and thinner in diameter than lateral lenticulostriate arteries in MCA58. In this study, they have a diameter of 0.4 mm, length of 20 mm and number 9 in total.
The A2 segment which starts at the AComA ranges through the frontal portion of lamina terminalis laterally to the corpus callosum rostrum, and terminates at the beginning of callosimarginal artery or corpus callosum genu. A2 is known as either the infracallosal, post-communicating or vertical segment of ACA. The main branches that arise from the A2 segment are the recurrent artery of Heubner (RAH), orbitofrontal artery (OFA) and frontopolar artery (FPA)53. The RAH which is also known as the distal medial striate artery originates either from the proximal part of A2 or the distal portion of A1; it has a mean length and radius of 24 mm and 0.7 mm (range is 0.2–2.9 mm), respectively51,59. The orbitofrontal arteries in the ACA segment are called medial orbitofrontal arteries (MOFA) with a mean number of 15 branches and a range of 2–28 branches in the ACA. The MOFA is located 7.9 mm anterior to the AComA with a mean diameter of 1 mm and a range of 0.2–2 mm48. The FPA is reported to have an average diameter of 1.02 ± 0.46 mm and an average length of 10.7 ± 5.1 mm from the beginning of FPA to AComA60.
The A3 segment of ACA is called the precallosal segment which is positioned distal to the origin of the callosomarginal artery (CMA), extending and turning around the corpus callosum genu and terminating above the rostral part of the corpus callosum51,53. The CMA is considered one of the prominent branches in the distal part of the ACA with a diameter ranging from 1.8 to 1.9 mm51. In this study, a mean diameter of 1.85 mm is established for CMA. The A4 segment of ACA is called a supracallosal segment which is positioned above the frontal portion of the corpus callosum body to the level of the coronal structure. Conversely, the A5 segment is called a post-callosal segment which is positioned above the latter portion of the corpus callosum body to the level of coronal structure53. The major branches arising from both these segments are the paracentral artery, inferior and superior parietal artery and posterior internal frontal artery51. Major studies report that it is very hard to determine the geometric parameters of distal and cortical branches of arteries from A3 to A5 segments because of the high variations in the origin, and diameter of these distal segments and branches51. However, a study reported the diameter of cortical branches ranges from 0.79 ± 0.27 mm to 1.84 ± 0.3 mm53. In this scenario, this study has given an assumed value for the diameters of A3, A4 and A5 as 2, 1.5 and 1 mm, respectively. Zhu et al.56 found the average total length of the distal segment of ACA is 250 mm. Considering this measurement and eliminating the length of A1 and A2 segments and other branches along with the distal segments, the A3, A4 and A5 segments are each assumed to be 30 mm in length.
Ophthalmic artery
The ophthalmic artery is one of the smallest branches arising from the ICA which supplies to the eye orbit and nearby structures. This artery extends through the orbital cavity and has 10 branches along its course. The branches of the ophthalmic artery are the central retinal artery, posterior ciliary arteries, muscular branches, lacrimal artery, medial palpebral arteries supraorbital artery, posterior and anterior ethmoidal artery, dorsal nasal artery, and supratrochlear artery61. Studies report that the central retinal artery has an average diameter and length of 0.16 mm and 7.5 ± 2.2 mm, respectively62,63. Considering the length of the central retinal artery, the posterior ciliary artery is given an assumed diameter of 0.1 mm, whereas the mean length of this artery is reported to be in the 3–7 mm range64. The remaining branches of the ophthalmic artery is not examined in this study as their geometrical parameters are too small to have any impact on the results of this study.
ECA segments
The main branches of ECA are the Superior thyroid artery, Lingual artery, Occipital artery, Maxillary artery, Ascending pharyngeal artery, Posterior auricular artery, Superficial temporal artery, and Facial artery65. Arjun et al. measured the diameter of the superior thyroid artery (STA) as 2 mm whereas in another study the diameter was 0.5–1.5 mm and the length 30 mm66,67,68. The ascending pharyngeal artery (AP) is located in the frontal position of the proximal side of the ECA with an average diameter of 1 mm and length of 70 mm67,69. The lingual artery is reported to have a diameter of 2–5 mm and a length which is approximately 75% that of the dorsal portion to the tip of the human tongue70,71. The mean length of the human tongue is 90 mm, so in this study, the length of the lingual artery is noted as 67.5 mm72. The mean diameter of the facial artery at the origin and anteroinferior angle of masseter is within the 3.0–3.2 mm range for both males and females whereas the mean length is 28 mm67,73,74. Ozkan et al.75 measured the mean thickness and length of the occipital artery (OA) as 1.9 mm and 79.3 mm, respectively. A study reported the range of diameter and length of the posterior auricular artery as 0.7–1.2 mm and 64 ± 13 mm, respectively76. The maxillary artery is estimated to have an average diameter of 4.08 ± 0.51 mm at the location of its branching from ECA and an average length of 80 mm67,77,78. Marano et al.79 reported the average diameter and length of the superficial temporal artery as 2.2 mm and 70 mm, respectively. Hiller et al.68 measured the averaged diameter of the proximal and distal ECA as 4 ± 0.6 mm and 2.85 ± 0.4 mm, respectively.
Windkessel parameter calculations of carotid artery segments
The Windkessel model is a zero-dimensional (0-D) one and it is analogous to the electrical circuit. Based on the mathematics of lumped parameter model,
whereas (mu) is the blood viscosity, (l) denotes the segment length, (D) is the diameter of the artery segment, (G) stands for Young’s modulus of the blood vessel and (h) represents the wall thickness of the blood vessel. Resistor with resistance (R) represents viscous friction experienced by the blood flow in the arterial system, especially at the blood-vessel interface of small arteries and arterioles. A resistor is arranged in two ways, either as proximal resistance (Rp) or distal resistance (Rd). Proximal resistance represents the viscous resistance of the proximal regions of the vasculature whereas distal resistance represents the resistance of the distal regions such as capillaries, arterioles, and venous circulation. The capacitor with capacitance (C) represents the compliance or elasticity of blood vessels17,23,24,25,26,80. In this study, we are considering a three-element Windkessel model (RCR) with proximal resistance (Rp), compliance (C) and distal resistance (Rd). The blood flow rate and pressure distribution at the outlet of the CFD model of the carotid artery using the RCR Windkessel model are shown by a partial differential equation (Eq. 3), which explains the relationship between current and voltage in the electrical circuits:
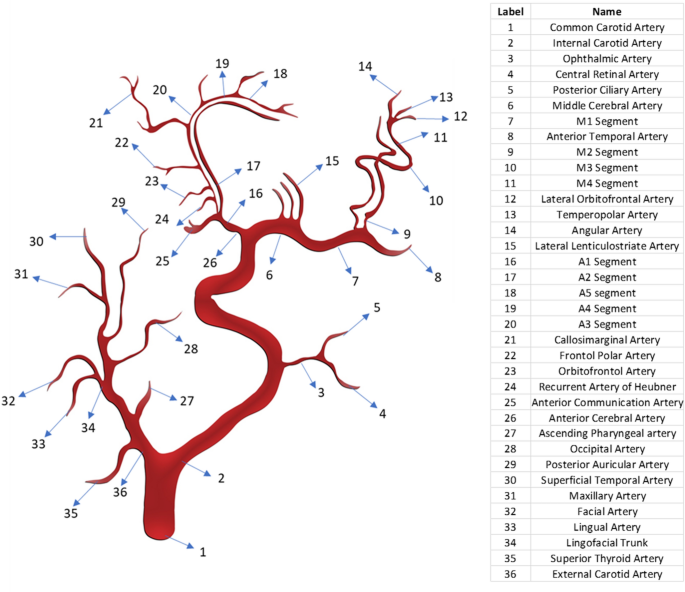
In Eq. (3), (Q) represents the blood flow rate which is similar to the current in the electrical circuits, whereas (P) represents the time-dependent blood pressure which is analogous to voltage in the electrical circuit. In this study, resistance R and compliance C of all the branches and sub-branches of the carotid artery are analytically calculated by using Eqs. (1 and 2). The results are listed in Table 1. The total proximal resistance, distal vascular resistance and compliance of the ICA and ECA branches were calculated based on the arrangement of the branches and sub-branches of the carotid artery in Fig. 1. Based on this arrangement, the decision is made to choose the series and parallel arrangement of the resistance and compliance of the carotid artery’s distal vascular elements. The total resistance and compliance of each branch are estimated based on the equivalent resistance and compliance in series or parallel conditions which are shown in Tables 2, 3, 4 and 5. In the next step, a CFD simulation was done to validate the analytically calculated values of resistance and compliance of branches of the CCA.
Mapping of distal vascular elements of the carotid artery.
CFD simulations and validation
In this study, validation of the analytical results on the Windkessel parameters was conducted by using computational fluid dynamics (CFD) simulations on two different geometries of carotid artery.
-
1.
A CFD simulation was performed on a simplified model of the carotid artery, utilizing the resistance and compliance values for the proximal sections of the internal carotid artery (ICA) and external carotid artery (ECA). The primary objective was to determine whether the analytically calculated Windkessel parameters accurately reflected the flow rate splits between ICA and ECA, in comparison to the generalized clinical flow split ratio.
-
2.
A CFD simulation was carried out on a patient-specific geometry of the ICA, with a particular emphasis on the distal sections including branches such as the Ophthalmic artery, Anterior Cerebral Artery (ACA), and Middle Cerebral Artery (MCA) segments (M1 and M2). This simulation incorporated the analytically calculated resistance and compliance values for these distal branches. The CFD results were then compared to the phase-contrast magnetic resonance imaging (PCMRI) data obtained from the patient. The PCMRI data included blood flow velocity measurements from the MCA and ACA after the ICA bifurcation.
CFD simulations on a simple carotid artery model
A CFD simulation was done on the carotid artery geometry to validate the results obtained in this study. The Windkessel parameters calculated in this study for both ICA and ECA are applied to this geometry and monitored the flow splits between ICA and ECA. The CFD simulation was done using the commercial software ANSYS Fluent 2022 b. A 3D model of the carotid artery provided by ANSYS Inc. was employed in this study. Meshing was done using Ansys meshing in the Workbench 2022 b version. The tetrahedron grid element was used in the meshing with a minimum element size of 0.4 mm which has a finer mesh with 294,255 mesh elements and 92,840 nodes. This mesh was chosen after conducting the mesh refinement study. Inflation layers were also given to the boundaries of the wall to enable refinement near the wall. Blood flow is assumed to be an incompressible laminar flow with Newtonian characteristics. Blood flow density is given as 1060 kg/m3 and viscosity as 0.004 Pa.s. A clinical blood flow rate was given as the inlet boundary condition which is obtained from one study81. This inlet blood flow rate was given to the CFD domain as a form of User Defined Function (UDF). The Windkessel-based outlet boundary conditions were given to the model based on analytically calculated values of the parameters resistance and compliance based on the results in Tables 1, 2, 3, 4, 5. The simulation time of the one cardiac cycle is given as 0.55 s based on the clinical data obtained from81 with an initial time step size of 0.001S. The simulation was done using the adaptive method with the solution convergence criteria of 10−6 for all variables. The simulation was done for 7 cardiac cycles and the blood volume flow rate split between the ICA and ECA branches is monitored from the CFD simulations. This captures the blood flow ratio of ICA and ECA with respect to the CCA blood flow rate. Figure 2 gives the representation of CFD model used in this study.

CFD model for simplified carotid artery used in this study.
CFD simulations on a patient specific internal carotid artery model
In this approach, a patient-specific 3D model of the internal carotid artery and PCMRI clinical results, provided by See-Mode Technologies Pte. Ltd., was utilized. The computational fluid dynamics (CFD) simulation was conducted using the commercial software ANSYS Fluent 2022 b. The meshing process was performed using Ansys Meshing in the Workbench 2022 b version. The tetrahedral grid element was employed, with a minimum element size of 0.3 mm, resulting in a finer mesh consisting of 431,468 mesh elements and 177,603 nodes. This mesh configuration was selected following a mesh refinement study. Inflation layers were added to the boundaries of the wall to allow for refinement near the wall.
The blood flow within the model was assumed to be incompressible, laminar, and exhibit non-Newtonian characteristics. The Carreau model was employed to incorporate these non-Newtonian properties, with the following parameter values: time constant of 3.313 s, Power-Law index of 0.3568, Zero Shear Viscosity of 0.056 kg/(ms), and Infinite Shear Viscosity of 0.0035 kg/(ms). The blood flow density was set to 1060 kg/m3. The patient-specific blood flow velocity measurements obtained from the internal carotid artery using the PCMRI technique were assigned as the inlet boundary condition. This inlet blood flow rate was implemented in the CFD domain using a User Defined Function (UDF). The outlet boundary conditions of the model, such as M1, M2, ACA, and the Ophthalmic artery, were defined based on analytically calculated values of the parameters resistance and compliance, as presented in Tables 1, 2, 3, 4, 5. The simulation time for one cardiac cycle was determined as 0.753 s, based on the PCMRI data, with an initial time step size of 0.01 s. The simulation was conducted using the adaptive method, with a solution convergence criterion of 10−6 for all variables. The simulation was performed over five cardiac cycles. Figure 3 gives the representation of CFD model used in this study.

CFD model used for patient specific internal carotid artery.
Results
In this study, resistance R and compliance C of all the branches and sub-branches of the carotid artery are analytically calculated using Eqs. (1 and 2); the results are listed in Table 1. The total proximal resistance, distal vascular resistance and compliance of the ICA and ECA branches were calculated based on the arrangement of the branches and sub-branches of the carotid artery in Fig. 1. Based on this arrangement, the decision is made on choosing the series and parallel arrangement of resistance and compliance of the carotid artery’s distal vascular elements. The total resistance and compliance of each branch are estimated based on the equivalent resistance and compliance in series or parallel conditions which are shown in Tables 2, 3, 4, 5. The proximal segment of the ICA has a resistance of 4.80E + 06 kg m−4 s−1 and compliance of 1.48E−12 kg−1m4 s2. The analytical method used calculating the compliance and resistance of the distal branches of ICA is shown in Tables 2 and 3. The total distal vascular resistance and compliance of the ICA branch are 5.89E + 07 kg m−4 s−1 and 3.79E−14 kg−1m4 s2, respectively. Referring to the ECA branch, Tables 4 and 5 show the analytical calculation method used for resistance and compliance. The proximal resistance and compliance of the ECA branch are 1.11E + 07 kg m−4 s−1 and 4.31E−13 kg−1m4 s2, respectively. The total distal vascular resistance and compliance of the ECA branch are 3.19E + 07 kg m−4 s−1 and 3.89E−13 kg−1m4 s2, respectively.
The aim of the first validation study is to calculate the volumetric flowrate split ratio using resistance and compliance as the outlet boundary conditions through the Windkessel model for the ECA and ICA outlets and compare it with clinical results. This is a crucial part of the validation process as the flow split ratio is sensitive to changes in outlet boundary conditions. If the calculated flow split ratio from CFD studies using these parameters matches clinical results, it demonstrates that the outlet boundary conditions given in this study are accurate.
To validate the results, the resistance and compliance values for the distal and proximal segments of both ICA and ECA branches are used in a CFD simulation with the Windkessel model outlet boundary conditions. The volumetric blood flow distribution for the CCA, ICA, and ECA branches from CFD simulations for 7 cardiac cycles is shown in Fig. 4. The average blood volume flow rates for the entire 7 cardiac cycles from CFD simulations for the CCA, ICA, and ECA branches are 5.35 cm3/s, 3.83 cm3/s, and 1.52 cm3/s, respectively. The calculated blood volume flow rate split between ICA and ECA with respect to CCA from this study is 71.55% and 28.45%, respectively. When comparing the blood flow split ratio results to clinical data regarding the blood flow splits between ICA and ECA, it is found to be a close match. The average blood flow split between ICA and ECA calculated based on the clinical results from study 82 is 70.55% and 29.45%, respectively. The error percentage between the CFD results in this study and the calculated flow rate split based on clinical results from82 is estimated as − 1.39% and 3.39% for ICA and ECA branches, respectively.

Volumetric blood flow distribution of branches of the carotid artery.
In the second validation study, the resistance and compliance values for the outlets (Ophthalmic artery, ACA, M1, and M2) were determined based on the values provided in Tables 1, 2, 3. The velocity of blood flow in the ACA branch was measured in four adjacent planes following the ICA bifurcation into the MCA and ACA. The area-weighted average of the velocity from these four planes over five cycles was calculated and depicted in Fig. 5. Similarly, the area-weighted average of blood velocity from the MCA branch was averaged over five planes and shown in Fig. 6. The measurement planes for both ACA and MCA in the CFD simulations corresponded to the same planes where the PCMRI data of the patient were collected. Figures 5 and 6 compare the velocity calculated in these simulations to the velocity obtained from the PCMRI data of the patients. From Fig. 5, it can be observed that the velocity values calculated for the ACA branch in the CFD simulations were slightly overestimated compared to the PCMRI values, with an average velocity difference of 0.051 m/s. The maximum velocity difference was 0.07 m/s at time instance 0.381 s, while the minimum velocity difference was 0.019 m/s at time instant 0.109 s. For the MCA branch, Fig. 6 demonstrates a better match between the velocity values obtained from CFD simulations and the PCMRI data. In this case, although the CFD velocity values were slightly underestimated in the first half of the cardiac cycle, they exhibited similar values to the PCMRI data in the second half of the cycle, with an average difference in velocity of 0.029 m/s for the full cycle. The maximum velocity difference was 0.064 m/s at time instance 0.163 s, while the minimum velocity difference was 0.004 m/s at time instance 0.653 s.

Average velocity distribution at ACA of patient specific internal carotid artery.

Average velocity distribution at MCA of patient specific internal carotid artery 1.
Discussion
Peripheral resistance of the distal vascular elements in the cerebrovascular system is very important because it wields a lot of influence on determining the flow partition at ECA and ICA of the carotid bifurcation. It also has a significant effect on the pressure and flow distribution inside the arteries83. Similarly, arterial compliance is an important parameter in the application of outlet boundary conditions. It is reported that arterial compliance has a strong influence on the estimation of wall shear stress particularly in flow separation regions and recirculation zones. The compliance property of the artery wall stretches the vessels continuously which leads to changes in the wall shear stress distribution84. Thus the incorporation of resistance and compliance is essential for obtaining accurate CFD simulation results.
In this study, the analytically calculated values for resistance and compliance for the distal branches of the carotid artery make it easier to incorporate the Windkessel model outlet boundary conditions into the CFD domain. Results show that the distal segment of the ICA and ECA branch has more resistance compared to the proximal segments because of the more constricted geometrical appearances in the distal segments of these branches. In the case of the ICA branch, of the major branches, the Ophthalmic artery offers the most resistance but considering its geometrical size and location it might not have much influence in deciding the hemodynamics of the carotid artery. The MCA and ACA being the largest and terminal distal branches of the ICA segment exert a huge influence in deciding the blood flow characteristics in the carotid artery. Results show that ACA contributes more resistance to the blood flow when compared to the MCA branch, yet for compliance, MCA has more compliant features compared with ACA.
Amongst the segments of ACA, the A5 segment provides more resistance to flow whereas the A1 segment provides the least resistance. Regarding the MCA segment, M4 shows the most resistance whereas the M1 segment provides the least. This indicates that distal segments become narrower as they are positioned away from the proximal segment of the carotid artery. With reference to compliance, proximal segments are more compliant compared to the distal segment. A1 segment of ACA is more compliant than the A5 segment, and similarly, the M1 segment is more compliant compared to the M4 segment. In the case of the ECA segment, the Posterior Auricular Artery exhibits the highest resistance and lowest compliance whereas the Maxillary Artery has the lowest resistance and highest compliance. Consequently, the results in this study give more opportunity to understand the distal vascular characteristics of the carotid artery branches.
The CFD simulations and clinical validation carried out in this study play a crucial role in determining the applicability of the findings to research aimed at understanding the hemodynamics of the carotid artery. The validation process involved two distinct approaches. Firstly, a simplified geometry of the carotid artery was utilized, relying on generalized clinical data to focus on the flow split ratio between the ICA and ECA. Secondly, a patient-specific geometry and clinical data were employed, with a particular emphasis on the velocity profiles in the distal sections of the ICA, such as the ACA and MCA.
As discussed in the results section, the simulations performed on the simplified geometry yielded flow partition values of 71.55% and 28.45% for the ICA and ECA branches, respectively, which closely aligned with the clinical flow partition results, exhibiting error percentages of − 1.39% and 3.39% for the ICA and ECA branches, respectively. It is important to note that the study was conducted using a healthy carotid artery, and the clinical validation data was also obtained from healthy individuals. The flow split ratio provides insights into the likelihood of downstream plaque or atherosclerotic vessels, with deviations from the established range indicating the presence of such conditions. Moreover, if the flow splits calculated from MRI differ from the results of this study, it may indicate the likelihood of atherosclerotic vessels.
The results from the patient-specific studies, focusing on the distal branches of the ICA, demonstrate that the use of analytically calculated values for the Windkessel parameters in this study yields matching velocity profiles when compared to PCMRI data. The average velocity difference for the ACA and MCA, compared to PCMRI data, is 0.05 m/s and 0.029 m/s, respectively. Although slight differences in velocity values may be observed at certain time instances, further iterations can yield matching velocity profiles, facilitating subsequent CFD simulations. It is important to note that this study does not expect a perfect match with patient-specific clinical results but rather offers a pathway for easier iterations to align with clinical data for any patient-specific geometries. Therefore, the CFD results from this study indicate that the analytically calculated values of the Windkessel parameters for the distal branches of the carotid artery can be utilized in studies focusing on distal branches, such as the MCA and ACA. These values of the Windkessel parameters, including resistance and compliance, can serve as initial values for iterations when aiming to align hemodynamic parameters obtained from CFD studies with clinical data. This helps reduce the time spent on iteration processes. Furthermore, this study provides resistance and compliance values for the major sub-branches and distal sections of the ACA and MCA, opening doors for researchers in this field to explore the hemodynamics of the distal cerebral vascular system. Consequently, researchers can eliminate numerous erroneous assumptions concerning outlet boundary conditions in these branches, leading to more accurate investigations.
Limitations
Although this study made the best effort to identify the distal resistances at ACA and MCA by incorporating all available information on the dimensions of distal arteries from previous works, we acknowledge that the lack of detailed information on the microvasculature dimensions in our study is a universal limitation of all CFD studies investigating strokes in the cerebral arteries. Nonetheless, with the advancements in high-resolution medical imaging techniques, we believe that our paper can serve as a starting point for exploring additional resistances and compliances further downstream of ACA, MCA, and ECA in future studies, ultimately improving the accuracy of resistance and compliance calculations.
Conclusion
Outlet boundary conditions are a very important parameter in determining the accuracy of CFD simulations. The Windkessel model outlet boundary condition is a prominent outlet boundary condition which can incorporate the distal vascular characteristics of the carotid artery into the CFD domain. The Windkessel parameters for the distal branches of the carotid artery calculated in this study through the analytical method are very relevant in obtaining more accurate CFD results. As well, the outcomes of this study give an easier option to establish the resistance and compliance of the distal branches of carotid artery. This is otherwise a tedious, time-consuming, and high computational cost operation that needs various iterations till matching with clinical results is achieved. The validation of the CFD results in this study against the clinical data confirms the relevant applicability of our findings to future studies aiming to comprehend the hemodynamics of cerebral arteries.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
-
Jun-Xuan, L. V. et al. Current advances in circulating inflammatory biomarkers in atherosclerosis and related cardio-cerebrovascular diseases. J. Chronic Dis. Transl. Med. 3(4), 207–212 (2017).
-
Sitzer, M. et al. Internal carotid artery angle of origin: A novel risk factor for early carotid atherosclerosis. Stroke 34(4), 950–955 (2003).
Google Scholar
-
Sakellarios, A. I. et al. Patient-specific computational modeling of subendothelial LDL accumulation in a stenosed right coronary artery: Effect of hemodynamic and biological factors. Am. J. Physiol. 304(11), H1455–H1470 (2013).
Google Scholar
-
Malek, A. M. et al. Hemodynamic shear stress and its role in atherosclerosis. Am. Med. Assoc. 282(21), 2035–2042 (1999).
Google Scholar
-
Fry, D. et al. Acute vascular endothelial changes associated with increased blood velocity gradients. Am. Heart Assoc. 22(2), 165–197 (1968).
Google Scholar
-
Ramstack, J. et al. Shear-induced activation of platelets. J. Biomech. 12(2), 113–125 (1979).
Google Scholar
-
Lee, S. H. et al. A fluid-structure interaction analysis on hemodynamics in carotid artery based on patient-specific clinical data. J. Mech. Sci. Technol. 26(12), 3821–3831 (2012).
Google Scholar
-
Karino, A. et al. Microscopic structure of disturbed flows in the arterial and venous systems, and its implication in the localization of vascular diseases. Int. Angiol.: J. Int. Union Angiol. 5(4), 297–313 (1986).
Google Scholar
-
Xu, P. et al. Assessment of boundary conditions for CFD simulation in human carotid artery. Biomech. Model. Mechanobiol. 17(6), 1581–1597 (2018).
Google Scholar
-
Markl, M. et al. In vivo wall shear stress distribution in the carotid artery: effect of bifurcation geometry, internal carotid artery stenosis, and recanalization therapy. Am. Heart Assoc. 3(6), 647–655 (2010).
-
Marshall, I. et al. MRI and CFD studies of pulsatile flow in healthy and stenosed carotid bifurcation models. J. Biomech. 37(5), 679–687 (2004).
Google Scholar
-
Tu, J. et al. Analysis of patient-specific carotid bifurcation models using computational fluid dynamics. J. Med. Imaging Health Inform. 1(2), 116–125 (2011).
Google Scholar
-
Moyle, K. R. et al. Inlet conditions for image-based CFD models of the carotid bifurcation: Is it reasonable to assume fully developed flow?. J. Biomech. Eng. 128(3), 371–379 (2006).
Google Scholar
-
Wake, A. K. et al. Choice of in vivo versus idealized velocity boundary conditions influences physiologically relevant flow patterns in a subject-specific simulation of flow in the human carotid bifurcation. J. Biomech. Eng. 131(2), 021013 (2009).
Google Scholar
-
Vignon-Clementel, I. E. et al. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput. Methods Appl. Mech. Eng. 195(29–32), 3776–3796 (2006).
Google Scholar
-
Groen, H. C. et al. MRI-based quantification of outflow boundary conditions for computational fluid dynamics of stenosed human carotid arteries. J. Biomech. 43(12), 2332–2338 (2010).
Google Scholar
-
Guan, D. et al. Comparison of the Windkessel model and structured-tree model applied to prescribe outflow boundary conditions for a one-dimensional arterial tree model. J. Biomech. 49(9), 1583–1592 (2016).
Google Scholar
-
Grinberg, L. et al. Large-scale simulation of the human arterial tree. Clin. Exp. Pharmacol. Physiol. 36(2), 194–205 (2009).
Google Scholar
-
Olufsen, M. S. et al. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann. Biomed. Eng. 28(11), 1281–1299 (2000).
Google Scholar
-
Du, T. et al. Outflow boundary conditions for blood flow in arterial trees. PLoS ONE 10(5), e0128597 (2015).
Google Scholar
-
Olufsen, et al. Structured tree outflow condition for blood flow in larger systemic arteries. Am. J. Physiol. 276(1), H257–H268 (1999).
Google Scholar
-
Reymond, P. et al. Validation of a one-dimensional model of the systemic arterial tree. Am. J. Physiol. 297(1), H208–H222 (2009).
Google Scholar
-
Paisal, M. S. A. et al. An analysis of blood pressure waveform using windkessel model for normotensive and hypertensive conditions in carotid artery. J. Adv. Res. Fluid Mech. Thermal Sci. 57(1), 69–85 (2019).
-
Westerhof, N. et al. The arterial windkessel. Med. Biol. Eng. Compu. 47(2), 131–141 (2009).
Google Scholar
-
Żyliński, M. et al. International Society for Optics and Photonics. Individualization of the parameters of the three-elements Windkessel model using carotid pulse signal. in Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2015, vol. 9662, 96621N, (2015).
-
Stergiopulos, N. et al. Total arterial inertance as the fourth element of the windkessel model. Am. J. Physiol. 276(1), H81–H88 (1999).
Google Scholar
-
Otto, F. et al. Die grundform des arteriellen pulses. Zeitung fur Biologie 37, 483–586 (1899).
-
Gerringer, J. W. et al. Lumped-parameter models of the pulmonary vasculature during the progression of pulmonary arterial hypertension. Physiol. Soc. 6(3), e13586 (2018).
-
Jonášová, A. et al. Noninvasive assessment of carotid artery stenoses by the principle of multiscale modelling of non-Newtonian blood flow in patient-specific models. Appl. Math. Comput. 319, 598–616 (2018).
Google Scholar
-
Olufsen, M. S. et al. Dynamics of cerebral blood flow regulation explained using a lumped parameter model. Am. J. Physiol. 282(2), R611–R622 (2002).
Google Scholar
-
Khan, A. S. et al. Personalized 0D models of normal and stenosed carotid arteries. Comput. Methods Programs Biomed. 200, 105888 (2021).
Google Scholar
-
Studinger, P. et al. Static and dynamic changes in carotid artery diameter in humans during and after strenuous exercise. J. Physiol. 550(2), 575–583 (2003).
Google Scholar
-
Kojo, M. et al. Normal developmental changes in carotid artery diameter measured by echo-tracking. Pediatr. Neurol. 18(3), 221–226 (1998).
Google Scholar
-
Arndt, J. O. et al. The diameter of the intact carotid artery in man and its change with pulse pressure. Eur. J. Physiol. 301(3), 230–240 (1968).
Google Scholar
-
Onaizah, O. et al. A model of blood supply to the brain via the carotid arteries: Effects of obstructive vs. sclerotic changes. Med. Eng. Phys. 49, 121–130 (2017).
Google Scholar
-
Phan, T. G. et al. Carotid artery anatomy and geometry as risk factors for carotid atherosclerotic disease. Stroke 43(6), 1596–1601 (2012).
Google Scholar
-
Kumar, N. et al. Computational fluid dynamic study on effect of Carreau-Yasuda and Newtonian blood viscosity models on hemodynamic parameters. J. Comput. Methods Sci. Eng. 19(2), 465–477 (2019).
-
Bouthillier, A. et al. Segments of the internal carotid artery: A new classification. Neurosurgery 38(3), 425–433 (1996).
Google Scholar
-
Rai, A. T. et al. Cerebrovascular geometry in the anterior circulation: an analysis of diameter, length and the vessel taper. J. NeuroIntervent. Surg. 5(4), 371–375 (2013).
Google Scholar
-
Hedayat, H. S. et al. Middle cerebral artery. In Intracranial aneurysms (ed. Ringer, A. J.) 527–537 (Elsevier, 2018). https://doi.org/10.1016/B978-0-12-811740-8.00031-9.
Google Scholar
-
Beger, A. Middle cerebral artery. Available: https://www.kenhub.com/en/library/anatomy/middle-cerebral-artery (2022, March 13).
-
Jones, J. Middle cerebral artery. Available: https://radiopaedia.org/articles/4522 (2008).
-
Idowu, O. et al. Size, course, distribution and anomalies of the middle cerebral artery in adult Nigerians. Esat Afr. Med. J. 79(4), 217–220 (2002).
Google Scholar
-
Reçi, V. et al. Variations of shape, length, branching, and end trunks of M1 segment of middle cerebral artery. J. Neurol. 5(1), 052–056 (2019).
-
Liem, M. K. et al. Lenticulostriate arterial lumina are normal in cerebral autosomal-dominant arteriopathy with subcortical infarcts and leukoencephalopathy: A high-field in vivo MRI study. Am. Heart Assoc. 41(12), 2812–2816 (2010).
-
Shakur, S. F. et al. Complications of cerebral bypass surgery. In Complications in neurosurgery (ed. Nanda, A.) 59–63 (Elsevier, 2019).
Google Scholar
-
Umansky, F. et al. Microsurgical anatomy of the proximal segments of the middle cerebral artery. Am. Assoc. Neurol. Surg. 61(3), 458–467 (1984).
Google Scholar
-
Mavridis, I. N. et al. The microsurgical anatomy of the orbitofrontal arteries. World Neurosurg. 89, 309–319 (2016).
Google Scholar
-
Oo, E. M. et al. Variable anatomy of the middle cerebral artery from its origin to the edge of the sylvian fissure: A direct fresh brain study. Sci. World J. https://doi.org/10.1155/2021/6652676 (2021).
Google Scholar
-
Gibo, H. et al. Microsurgical anatomy of the middle cerebral artery. Am. Assoc. Neurol. Surg. 54(2), 151–169 (1981).
Google Scholar
-
de Sousa, A. A. et al. Distal anterior cerebral artery aneurysms. Surg. Neurol. 52(2), 128–136 (1999).
Google Scholar
-
Stefani, M. A. et al. Anatomic variations of anterior cerebral artery cortical branches. Clin. Anat. 13(4), 231–236 (2000).
Google Scholar
-
Gaillard, F. Anterior cerebral artery. Accessed 17 March 2022; https://radiopaedia.org/articles/4803 (2008).
-
Sharma, A. K. et al. A cadaveric anatomical study on anterior communicating artery aneurysm surgery by extended endoscopic endonasal approach. J. Neurosurg. 15(4), 908 (2020).
-
Gunnal, S. A. et al. Variations of anterior cerebral artery in human cadavers. Neurology Asia 18(3), 249–259 (2013).
-
Zhu, G. et al. Experimental study of hemodynamics in the circle of Willis. Biomed. Eng. Online 14(1), 1–15 (2015).
Google Scholar
-
Kakou, M. et al. Microanatomy of the pericallosal arterial complex. J. Neurosurg. 93(4), 667–675 (2000).
Google Scholar
-
R. G. MD. Lenticulostriatearteries. Available: https://www.kenhub.com/en/library/anatomy/lenticulostriate-arteries (2022).
-
Lopez, M. et al. Anatomy, head and neck, striate arteries. NCBI-national center for biotechnology information. (StatPearls Publishing LLC, 2021).
-
Najera, E. et al. Proximal branches of the anterior cerebral artery: anatomic study and applications to endoscopic endonasal surgery. Op. Neurosurg. 16(6), 734–742 (2019).
Google Scholar
-
G. S. MD. Ophthalmic artery. Available: https://www.kenhub.com/en/library/anatomy/ophthalmic-artery (2022).
-
Erdogmus, S. et al. Topography of the posterior arteries supplying the eye and relations to the optic nerve. Acta Ophthalmol. 84(5), 642–649 (2006).
Google Scholar
-
Dorner, G. T. et al. Calculation of the diameter of the central retinal artery from noninvasive measurements in humans. Taylor Francis Online 25(6), 341–345 (2002).
-
Department of ophthalmology and visual sciences, University of Iowa Hospitals and Clinics Iowa City, IA, USA. The Posterior Ciliary Artery. Available: https://entokey.com/the-posterior-ciliary-artery/#CR82 (2016)
-
Sieroslawska, A. External carotid artery and its branches. Available: https://www.kenhub.com/en/library/anatomy/the-external-carotid-artery-and-its-branches (2022).
-
Burlakoti, A. et al. Bilateral variant thyroid arteries. Int. J. Anat. Var. 8, 43–46 (2015).
-
Rajeev Mukhia, D. et al. Anatomical variations in the branches of external carotid artery in cadavers of nepalese origin. J. Human Anat. 4(1), 1–6 (2020).
Google Scholar
-
Hiller, A. et al. Recipient vessel selection in head and neck reconstruction. Eplasty 17, e42 (2017).
Google Scholar
-
Neuroangio.org. Ascending Pharyngeal Artery. Accessed 18 May 2022 http://neuroangio.org/anatomy-and-variants/ascending-pharyngeal-artery/ (2022).
-
Lettau, J. et al. Anatomy, head and neck, lingual artery. J. Eplasty (2021).
-
Mukherji, S. K. et al. Malignancies of the oral cavity, oropharynx, and hypopharynx. in Oncologic Imaging. 202-231, (Elsevier, 2002).
-
Sanders, I. et al. The human tongue slows down to speak: muscle fibers of the human tongue. Am. Assoc. Anatomy 296(10), 1615–1627 (2013).
-
Quadros, L. S. et al. Facial artery on face-a study on South Indian cadavers and specimens. J. Health Allied Sci. 3(03), 072–076 (2013).
Google Scholar
-
Lee, S.-H. et al. External and internal diameters of the facial artery relevant to intravascular filler injection. J. Am. Soc. Plast. Surg. 143(4), 1031–1037 (2019).
Google Scholar
-
Ateş, Ö. et al. The occipital artery for posterior circulation bypass: Microsurgical anatomy. Neurol. Focus 24(2), E9 (2008).
Google Scholar
-
Spetzler, R. F. et al. Vascular considerations in neurotologic surgery. in Otologic surgery, 799–814 (Elsevier Inc, 2010).
-
Wandee, D. et al. Anatomical study of the maxillary artery at the pterygomaxillary fissure in a Thai population: Its relationship to maxillary osteotomy. J. Med. Assoc. Thailand 87(10), 1212–1217 (2004).
-
Uysal, I. I. et al. Clinical significance of maxillary artery and its branches: A cadaver study and review of the literature. Web of Science ve Scopus Atıf Dizinlerindeki Yayınlar 29(4), 1274–1281. https://doi.org/10.4067/S0717-95022011000400034 (2011).
Google Scholar
-
Marano, S. R. et al. Anatomical study of the superficial temporal artery. Neurosurgery 16(6), 786–790 (1985).
Google Scholar
-
Madhavan, S. et al. The effect of inlet and outlet boundary conditions in image-based CFD modeling of aortic flow. Biomed. Eng. Online 17(1), 66 (2018).
Google Scholar
-
Vignon-Clementel, I. E. et al. Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput. Methods Biomech. Biomed. Engin. 13(5), 625–640 (2010).
Google Scholar
-
Zarrinkoob, L. et al. Blood flow distribution in cerebral arteries. J. Cereb. Blood Flow Metab. 35(4), 648–654 (2015).
Google Scholar
-
Balossino, R. et al. Computational models to predict stenosis growth in carotid arteries: Which is the role of boundary conditions?. Comput. Methods Biomech. Biomed. Engin. 12(1), 113–123 (2009).
Google Scholar
-
Malvè, M. et al. Impedance-based outflow boundary conditions for human carotid haemodynamics. Comput. Methods Biomech. Biomed. Engin. 17(11), 1248–1260 (2014).
Google Scholar
Author information
Authors and Affiliations
Contributions
M.K. mapped the distal branches of carotid artery, conducted Windkessel-based analytical calculations, conducted Computational Fluid Dynamics simulations (CFD)and wrote the article. J.S. contributed to CFD simulations, checking the validation of CFD results, editing and writing article, and oversaw and administrated the research. S.G. contributed to Windkessel-based analytical calculations, CFD simulations, editing and writing the article, oversaw and administrated the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Kizhisseri, M., Gharaie, S. & Schluter, J. An analytical method informed by clinical imaging data for estimating outlet boundary conditions in computational fluid dynamics analysis of carotid artery blood flow.
Sci Rep 13, 14973 (2023). https://doi.org/10.1038/s41598-023-42004-5
-
Received: 08 December 2022
-
Accepted: 04 September 2023
-
Published: 11 September 2023
-
DOI: https://doi.org/10.1038/s41598-023-42004-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.